Knowledge
1. Mathematics
1.1. Linear Algebra
主对角线上元素均为1其余位置均为0的方阵称为单位矩阵。
给定矩阵\(\boldsymbol{A} \in \mathbb{R}^{n \times n}\),如果存在矩阵\(\boldsymbol{B} \in \mathbb{R}^{n \times n}\)满足\(\boldsymbol{A}\boldsymbol{B} = \boldsymbol{I}_n = \boldsymbol{B}\boldsymbol{A}\), 则\(\boldsymbol{B}\)被称为\(\boldsymbol{A}\)的逆矩阵,记作\(\boldsymbol{A}^{-1}\).
对于矩阵\(\boldsymbol{A} \in \mathbb{R}^{m \times n}\),满足\(b_{ij} = a_{ji}\)的矩阵\(\boldsymbol{B} \in \mathbb{R}^{n \times m}\)被称为\(\boldsymbol{A}\)的转置,记作\(\boldsymbol{B} = \boldsymbol{A}^{\top}\).
矩阵\(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)如果满足\(\boldsymbol{A} = \boldsymbol{A}^\top\),则称其为对称矩阵。
考虑集合\(\mathcal{G}\)及定义在其上的运算\(\otimes\): \(\mathcal{G} \times \mathcal{G} \to \mathcal{G}\),则\(G := (\mathcal{G}, \otimes)\)在满足下列条件的情况下被称为群:
- 闭包性(closure): \(\forall x, y \in \mathcal{G}: x \otimes y \in \mathcal{G}\).
- 结合性(associativity): \(\forall x, y, z \in \mathcal{G}: (x \otimes y) \otimes z = x (y \otimes z)\).
- 单位元(neutral element): \(\exists e \in \mathcal{G}, \forall x \in \mathcal{G}: x \otimes e = x, e \otimes x = x\).
- 逆元(inverse element): \(\forall x \in \mathcal{G}, \exists y \in \mathcal{G}: x \otimes y = e, y \otimes x = e\).
一个实值向量空间(vector space)\(V = (\mathcal{V}, +, \cdot)\)是由集合\(\mathcal{V}\)及定义在其上的两种运算\(+: \mathcal{V} + \mathcal{V} \to \mathcal{V}\)和\(\cdot: \mathbb{R} \cdot \mathcal{V} \to \mathcal{V}\),且满足下列条件:
- \((\mathcal{V}, +)\)是一个阿贝尔群(交换群)。
- 乘法分配性
- \(\forall \lambda \in \mathbb{R}, \boldsymbol{x}, \boldsymbol{y} \in \mathcal{V}: \lambda \cdot (\boldsymbol{x} + \boldsymbol{y}) = \lambda \cdot \boldsymbol{x} + \lambda \cdot \boldsymbol{y}\).
- \(\forall \lambda, \psi \in \mathbb{R}, \boldsymbol{x} \in \mathcal{V}: (\lambda + \psi) \cdot \boldsymbol{x} = \lambda \cdot \boldsymbol{x} + \psi \cdot \boldsymbol{x}\).
- 乘法结合性: \(\forall \lambda, \psi \in \mathbb{R}, \boldsymbol{x} \in \mathcal{V}: \lambda \cdot (\psi \cdot \boldsymbol{x}) = (\lambda \cdot \psi) \cdot \boldsymbol{x}\).
- 乘法单位元: \(\forall \boldsymbol{x} \in \mathcal{V}: 1 \cdot \boldsymbol{x} = \boldsymbol{x}\).
考虑向量空间\(V = (\mathcal{V}, +, \cdot)\)及集合\(\mathcal{U} \subseteq \mathcal{V}, \mathcal{U} \neq \emptyset\),如果\(U = (\mathcal{U}, +, \cdot)\)满足向量空间的定义,那么向量空间\(U\)被称为向量空间\(V\)的向量子空间(vector subspace)或线性子空间(linear subspace),记作\(U \subseteq V\)。
由向量集合\(\mathcal{A} = \{\boldsymbol{x}_1, \dots, \boldsymbol{x}_k\}\)中元素的所有的线性组合组成的集合叫做\(\mathcal{A}\)的生成(span),记作\(\operatorname{span}[\mathcal{A}]\)。该向量集合\(\mathcal{A}\)称为由其生成的向量空间\(V = (\operatorname{span}[\mathcal{A}], +, \cdot)\)的生成集(spanning set)。
向量空间\(V = (\mathcal{V}, +, \cdot)\)的最小生成集\(\mathcal{A} \subseteq \mathcal{V}\)(无法由更小的集合\(\tilde{\mathcal{A}} \subseteq \mathcal{A} \subseteq \mathcal{V}\)生成)被称为它的基(Basis)。
1.2. Statistics
1.2.1. Probability space
一个概率空间(probability space) 1 由三元组\((\Omega, \mathcal{F}, P)\)定义:
- 样本空间(sample space)\(\Omega\):一个非空集合。表示一次实验所有可能输出值的集合。
- 事件空间(event space)\(\mathcal{F}\):集合\(\Omega\)上的\(\sigma\)代数(\(\sigma\)-algebra),即集合\(\Omega\)的子集的集合。表示由样本组成的事件。
- 概率测度(probability measure)\(P\):一个从事件空间\(\mathcal{F}\)映射到\([0,1]\)实数空间的函数。表示各个事件发生的概率。
1.2.2. Entropy
随机变量\(X\)取值为\(x\)的香农信息量(Shannon information content)或者也被称为自信息(self-information)定义为:
\begin{equation*} h(x) = \log_2\frac{1}{P(x)} \end{equation*}在此基础上,随机变量\(X\)的熵(entropy)被定义为其所有可能取值的期望香农信息量:
\begin{equation*} H(X) = \Sigma_{x \in \mathcal{A}_X}P(x) \log_2 \frac{1}{P(x)} \end{equation*}概率分布\(P(x)\)相对于\(Q(x)\)的相对熵(relative entropy)或者叫KL散度(Kullback-Leibler divergence)定义为:
\begin{equation*} D_{\text{KL}}(P \| Q) = \Sigma_x P(x) \log \frac{P(x)}{Q(x)} \end{equation*}相对熵满足吉布斯不等式(Gibbs' inequality):
\begin{equation*} D_{\text{KL}}(P \| Q) \geq 0 \end{equation*}2. Programming Languages
2.1. C/C++
2.1.1. STL常用容器
#include <iostream> #include <vector> #include <list> #include <stack> #include <queue> #include <set> #include <map> using namespace std; int main() { // vector std::vector<int> x_vector = {1, 2, 3}; x_vector.pop_back(); x_vector.emplace_back(4); cout << "vector member (random access): " << x_vector[1] << endl; cout << "vector first member: " << x_vector.front() << endl; cout << "vector last member: " << x_vector.back() << endl; // list std::list<int> x_list = {1, 2, 3}; x_list.pop_front(); x_list.emplace_front(0); x_list.pop_back(); x_list.emplace_back(4); cout << "list first member: " << x_list.front() << endl; cout << "list last member: " << x_list.back() << endl; // stack std::stack<int> x_stack({1, 2, 3}); x_stack.pop(); x_stack.emplace(4); cout << "stack member: " << x_stack.top() << endl; // queue std::queue<int> x_queue({1, 2, 3}); x_queue.pop(); x_queue.emplace(4); cout << "queue front member: " << x_queue.front() << endl; cout << "queue back member: " << x_queue.back() << endl; // set std::set<int> x_set = {1, 2, 3}; x_set.emplace(4); if (x_set.count(4)) cout << "set count test" << endl; // map std::map<int, int> x_map({{1, 11}, {2, 22}, {3, 33}}); x_map.emplace(4, 44); if (x_map.count(4)) cout << "map count test" << endl; return 0; }
3. DevOps
3.1. Git
3.1.1. 介绍
相比于以SVN为代表的集中式版本控制系统,Git所代表的分布式版本控制系统的主要优势体现在不存在“中央服务器”来进行版本记录,每个客户端都保存完整的版本库。
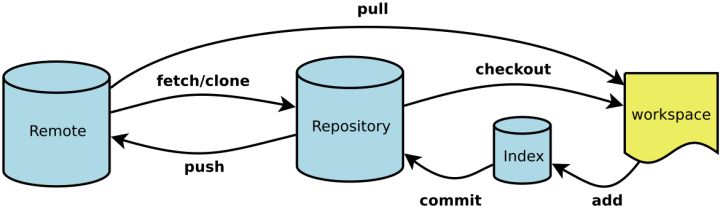
3.1.2. 用法
- 基本操作
git status git log
# 添加工作区的某个修改至暂存区 git add foo.txt # 将暂存区提交至本地仓库 git commit -m "msg" # 将本地仓库提交至远程仓库 git push
- 版本回退
# 回退一次提交 git reset HEAD^ # 回退两次提交 git reset HEAD^^ # 回退1000次提交 git reset HEAD~1000
- 放弃修改
如果修改还未加入暂存区
git checkout -- foo.txt
如果已经加入暂存区但是未提交至本地分支
# 将修改从暂存区拉回至工作区,之后就是上一种情况了 git reset HEAD foo.txt
如果已经提交到了本地分支,那么可以通过回退至上一个版本来实现放弃更改。
git reset HEAD^
- 修改历史
历史提交的修改通常是用rebase操作来进行的:
# 交互式地展示最近三次提交记录 git rebase -i HEAD~3 # 交互式地展示所有历史提交记录 git rebase -i --root
在rebase界面下我们可以很方便地对提交进行修改,注意某些修改可能会造成冲突,需要手动解决。
- 改变提交历史对应行的顺序可以直接反映到提交的历史上。
- 将
pick修改为d以删除某次提交。 - 将
pick修改为r以修改某次提交信息。 - 将
pick修改为e可以暂时进入指定的提交进行修改。
# 完成本次修改并继续rebase操作 git rebase --continue # 放弃本次修改 git rebase --abort
- 标签
# 打上标签 git tag tagName # 将标签更新至远程仓库 git push --tags # 删除本地标签 git tag -d tagName # 删除远程仓库标签 git push --delete origin tagName
3.2. zip
# -r: 选项表示递归地遍历目录 # -9: 表示压缩等级,缺省为6,数字越大压缩比例越高 zip foo.zip -r -9 foo
unzip foo.zip
3.3. tar
| 参数 | 描述 |
|---|---|
-c |
创建打包文件。常用 -z 指定gzip压缩来配合该选项。 |
-x |
与 -c 选项相反的操作,从打包文件中释放文件。 |
-f |
指定打包/解包的文件。 |
-v |
输出命令执行的详细信息。 |
# 仅打包 tar -cf foo.tar foo # 打包并压缩 tar -zcf foo.tgz foo # 解包/解压缩 tar -xf foo.tgz
3.4. GnuPG
| 参数 | 描述 |
|---|---|
-k |
列出公钥。 |
-K |
列出私钥。 |
-s |
签名。 |
-e |
加密。 |
-r |
指定接收者。 |
-c |
对称加密 |
-a |
设置为ASCII输出。 |
-d |
解密。 |
-o |
指定输出文件。 |
--clear-sign |
明文签名。 |
# 使用管道输入待加密数据并进行简单的对称加密 echo "bar bar" | gpg -ca - # 用用户名为chris的公钥加密并签名 gpg -rs chris -e foo.txt # 明文签名 gpg --clear-sign foo.txt # 解密及验证签名 gpg -d foo.txt.gpg
3.5. mutt
3.5.1. 基本配置
set imap_user = "name@aol.com" set imap_pass = "your-password" set smtp_url = "smtp://name\@aol.com@smtp.aol.com:587/" set smtp_pass = "your-password" set folder = "imaps://imap.aol.com:993" set spoolfile = "+INBOX"
3.5.2. 发送邮件
| 参数 | 描述 |
|---|---|
-s |
指定邮件标题。 |
-a |
添加附件(注意该参数务必置于 -- 参数前作为命令行选项的结尾)。 |
-c |
指定一个CC收件人。 |
-b |
指定一个BCC收件人。 |
-- |
将余下参数视作收件人邮箱地址。 |
mutt -s "Subject here" -a foo.png bar.jpg -- recipient1@gmail.com recipient2@gmail.com < foo.txt
3.5.3. 操作邮件
| 参数 | 描述 |
|---|---|
s |
保存邮件(删除当前位置的副本)。 |
<Esc>s |
解码并保存邮件(删除当前位置的副本)。 |
C |
复制邮件。 |
<Esc>C |
解码并复制邮件。 |
$ |
同步更改至邮箱。 |
3.6. bc
bc是GNU开发的一个任意精度的计算器语言,很多发行版都会自带,通过加 bc -l 参数启动后可以载入数学库。
| Function | Description |
|---|---|
% |
取余数 |
^ |
次方 |
sqrt(x) |
平方根函数 |
pi |
圆周率 |
| Function | Description |
|---|---|
s(x) |
sin |
c(x) |
cosine |
a(x) |
arctangent |
l(x) |
natural logarithm |
e(x) |
exponential |
j(n,x) |
bessel function |
4. Text Editors
4.1. Emacs
4.1.1. Dired
| Key | Description |
|---|---|
d |
标记删除 |
x |
删除标记文件 |
D |
删除文件 |
C |
复制文件 |
R |
重命名/移动文件 |
+ |
创建文件夹 |
w |
拷贝文件名 |
M-0 w |
拷贝文件绝对路径 |
W |
打开文件 |
4.1.2. Speedbar
| Key | Description |
|---|---|
g |
刷新 |
b |
切换到“缓冲区视图” |
k |
移除该缓冲区 |
r |
重载该缓冲区 |
f |
切换到“文件视图” |
<SPC> |
展开/闭合文件夹 |
D |
删除文件 |
C |
复制文件 |
R |
重命名/移动文件 |
4.2. Vim
4.2.1. 可配置选项
Vim中的可配置选项根据值的类型分为三类:
- 布尔型: 开或者关。
- 数字型: 整型数字值。
- 字符串型: 字符串值。
对于所有可配置选项均可以通过在配置名称后加 ? 来查看其当前值;加 & 来恢复其默认值。对于布尔型选项比较特殊,以行号显示的配置 number 举例:
| Command | Description |
|---|---|
:set number |
设置为“开” |
:set nonumber |
设置为“关” |
:set invnumber / :set number! |
切换状态 |
:set number? |
查看当前状态 |
:set number& |
恢复默认状态 |
4.2.2. 寄存器
- 命令
:reg可以显示所有寄存器及各自内容,命令后加参数可以指定显示哪些寄存器。 - 普通模式下可以通过
"来引用寄存器,比如:"ayy即可复制当前行到寄存器a中;"ap即可将寄存器a中的内容粘贴到当前位置。 - 插入模式下可以通过
<C-r>来引用寄存器,比如:<C-r>a即可插入寄存器a中的内容到当前位置。 - 用小写字母引用有名寄存器会覆盖该寄存器原有内容,而用大写字母则会将新内容添加到该寄存器的原有内容之后。
- 特殊寄存器:
": 无名(默认)寄存器。0: 复制专用寄存器,只有通过复制命令得到的内容才会被放入到该寄存器。=: 表达式寄存器,引用该寄存器可以输入数学表达式后插入运算结果。_: 黑洞寄存器,放入该寄存器的内容将立刻消失。+: 与系统剪贴板共享。
- 只读寄存器:
.: 该寄存器保存最近插入的文本内容。%: 该寄存器保存当前文件名。:: 该寄存器保存最近运行命令。#: 该寄存器保存最近访问文件(alternate-file)。
5. Data structure and algorithms
5.1. Tree data structure
5.1.1. Huffman tree
- 将\(w_1, w_2, \cdots, w_n\)看成是有\(n\)棵树的森林,每棵树仅有一个节点。
- 在森林中选出两个根节点的权值最小的树合并,作为一棵新树的左右子树,且新树的根节点权值为其左右子树根节点权值之和。
- 从森林中删除选取的两棵树,并将新树加入森林。
- 重复2、3两步,直到森林中只剩一棵树为止,该树即为所求Huffman树。
5.2. Sorting algorithms
| Algorithm | Smallest time | Average time | Largest time | Space complexity |
|---|---|---|---|---|
| Quicksort | \(\Omega(n\log(n))\) | \(\Theta(n\log(n))\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(\log(n))\) |
| Mergesort | \(\Omega(n\log(n))\) | \(\Theta(n\log(n))\) | \(\mathcal{O}(n\log(n))\) | \(\mathcal{O}(n)\) |
| Heapsort | \(\Omega(n\log(n))\) | \(\Theta(n\log(n))\) | \(\mathcal{O}(n\log(n))\) | \(\mathcal{O}(1)\) |
| Bubble sort | \(\Omega(n)\) | \(\Theta(n^2)\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(1)\) |
| Selection sort | \(\Omega(n^2)\) | \(\Theta(n^2)\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(1)\) |
| Tree sort | \(\Omega(n\log(n))\) | \(\Theta(n\log(n))\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(n)\) |
| Insertion sort | \(\Omega(n)\) | \(\Theta(n^2)\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(1)\) |
| Shell sort | \(\Omega(n\log(n))\) | \(\Theta(n(\log(n))^2)\) | \(\mathcal{O}(n(\log(n))^2)\) | \(\mathcal{O}(1)\) |
| Bucket sort | \(\Omega(n+k)\) | \(\Theta(n+k)\) | \(\mathcal{O}(n^2)\) | \(\mathcal{O}(n)\) |
| Radix sort | \(\Omega(nk)\) | \(\Theta(nk)\) | \(\mathcal{O}(nk)\) | \(\mathcal{O}(n+k)\) |
| Counting sort | \(\Omega(n+k)\) | \(\Theta(n+k)\) | \(\mathcal{O}(n+k)\) | \(\mathcal{O}(k)\) |
5.2.1. Quicksort
快排的步骤:
- 从待排序列中选一个元素作为基准(pivot);
- 重排序列,将比基准小的放到基准前面,比它大的放到基准后面;
- 递归地对基准前后的两个子序列进行重新排序。
def quickSort(s): if len(s) <= 1: return s left = [] right = [] for x in s[1:]: if x <= s[0]: left.append(x) else: right.append(x) return quickSort(left) + [s[0]] + quickSort(right)
5.2.2. Mergesort
归并排序的步骤:
- 把待排序列分成多个最小的子序列,仅包含一个元素的序列视为已排序序列。
- 重复地合并两个已排序的序列为一个,直到仅剩一个序列。
def mergeSort(s): # merge two sorted lists to one def merge(s1, s2): s = [] i = 0; j = 0 while i < len(s1) and j < len(s2): if s1[i] < s2[j]: s.append(s1[i]) i += 1 else: s.append(s2[j]) j += 1 return s + s1[i:] + s2[j:] if len(s) <= 1: return s m = len(s) // 2 left = mergeSort(s[:m]) right = mergeSort(s[m:]) return merge(left, right)
5.2.3. Heapsort
堆排序基于堆(heap)的数据结构,相当于一棵完全二叉树(complete binary tree),大顶堆(相反的还有小顶堆)的特性是父节点值总大于子节点。排序的步骤:
- 将待排序列构成一个大顶堆:依次从底层到顶层进行适当的父子节点值交换,保证父节点值总大于子节点。
- 将根节点(最大值)与末端节点交换,这样最大值就被交换到了序列最后。
- 将末端节点除外的堆继续从步骤1开始进行。
def heapSort(s): # max_heapify def siftDown(start, end): root = start while True: child = 2 * root + 1 # left child if child > end: break # right child if child + 1 <= end and s[child] < s[child + 1]: child += 1 if s[root] < s[child]: s[root], s[child] = s[child], s[root] root = child else: break n = len(s) - 1 # build max heap for start in range(n // 2, -1, -1): siftDown(start, n) # heapsort for end in range(n, 0, -1): s[0], s[end] = s[end], s[0] siftDown(0, end - 1) return s
5.2.4. Bubble sort
冒泡排序的步骤:
- 将待排序列从头开始两两比较,如果前一个比后一个大,则交换两者位置。
- 当交换至序列末尾时,序列最大的元素就到了序列尾部。
- 将除去尾部的序列重新重复步骤1,直到仅剩一个元素位置。
void bubbleSort(vector<int>& nums) { int n = (int) nums.size(); for (int i = 0; i < n; i++) { for (int j = 0; j < n-1; j++) { if (nums[j] > nums[j+1]) swap(nums[j], nums[j+1]); } } }
5.2.5. Selection sort
选择排序的步骤:
- 从待排序列中选取最小元素,存放到排序序列的起始位置。
- 从剩下的序列中选择最小元素,存放到排序序列的最后位置。
- 重复步骤2,知道没有剩余元素。
void selection_sort(int * arr, int len) { int i, j; int tmp; for (i = 0; i < len - 1; i++) { int min = i; for (j = i + 1; j < len; j++) { if (arr[j] < arr[min]) min = j; } tmp = arr[min]; arr[min] = arr[i]; arr[i] = tmp; } }
5.2.6. Tree sort
利用二叉搜索树(binary search tree)的一种排序方法,二叉搜索树的性质如下:
- 若左子树不空,则左子树上的节点值均小于或等于它的根节点。
- 若右子树不空,则右子树上的节点值均大于或等于它的根节点。
- 左、右子树也分别为二叉排序树。
data Tree a = Leaf | Node (Tree a) a (Tree a)
insert :: Ord a => a -> Tree a -> Tree a
insert x Leaf = Node Leaf x Leaf
insert x (Node t y s)
| x <= y = Node (insert x t) y s
| x > y = Node t y (insert x s)
flatten :: Tree a -> [a]
flatten Leaf = []
flatten (Node t x s) = flatten t ++ [x] ++ flatten s
treesort :: Ord a => [a] -> [a]
treesort = flatten . foldr insert Leaf
5.2.7. Insertion sort
插入排序的步骤:
- 将第一个元素视为已排序的序列。
- 从剩余元素依次取出元素插入到已排序的序列,构成新序列。
- 直到没有剩余未排序的元素。
def insertionSort(s): if len(s) <= 1: return s for i in range(1, len(s)): for j in range(i, 0, -1): if s[j] < s[j-1]: s[j], s[j-1] = s[j-1], s[j] else: break return s
5.2.8. Shell sort
void shell_sort(int arr[], int len) { int gap, i, j; int tmp; for (gap = len >> 1; gap > 0; gap >>= 1) { for (i = gap; i < len; i++) { tmp = arr[i]; for (j = i - gap; j >= 0 && arr[j] > tmp; j -= gap) { arr[j + gap] = arr[j]; } arr[j + gap] = tmp; } } }
5.2.9. Bucket sort
def bucket_sort(datalist): buckets = [0] * ((max(datalist) - min(datalist)) + 1) for i in range(len(datalist)): buckets[datalist[i] - min(datalist)] += 1 B = [] for i in range(len(buckets)): if buckets[i] != 0: B += [i + min(datalist)] * buckets[i] return B
5.2.10. Radix sort
基数排序是一种非比较型整数排序算法,其原理是将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
import math def radix_sort(l, radix = 10): k = int(math.ceil(math.log(max(l) + 1, radix))) for i in range(1, k+1): bucket = [[] for _ in range(radix)] for v in l: bucket[v%(radix**i) // (radix**(i-1))].append(v) l = [] for e in bucket: l.extend(e) return l
5.2.11. Counting sort
def counting_sort(a): k = max(a) n = len(a) b = [0 for i in range(n)] c = [0 for i in range(k + 1)] for j in a: c[j] = c[j] + 1 for i in range(1, len(c)): c[i] = c[i] + c[i-1] for j in a: b[c[j] - 1] = j c[j] = c[j] - 1 return b
6. Machine learning
6.1. The Gaussian Distribution
高斯分布的概率密度函数如下
\begin{equation*} \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma}) = \frac{1}{(2\pi)^{D/2}\left|\boldsymbol{\Sigma}\right|^{1/2}}\exp{\{-\frac{1}{2}(\boldsymbol{x} - \boldsymbol{\mu})^{\top}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x} - \boldsymbol{\mu})\}} \end{equation*}自变量\(\boldsymbol{x}\)以如下的二次项出现在指数中:
\begin{equation*} \Delta^2 = (\boldsymbol{x} - \boldsymbol{\mu})^{\top}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x} - \boldsymbol{\mu}) \end{equation*}如此定义的\(\Delta\)表示的是从\(\boldsymbol{\mu}\)到变量\(\boldsymbol{x}\)的马氏距离(Mahalanobis distance),而当\(\boldsymbol{\Sigma}\)是单位矩阵的时候,其退化为欧式距离(Euclidean distance)。
下面我们考虑协方差矩阵的特征向量\(\boldsymbol{u}_i\)及其特征值\(\lambda_i\),因为\(\boldsymbol{\Sigma}\)是实对称矩阵,固有下式成立,具体证明一并附上:
\begin{equation*} \boldsymbol{\Sigma} = \Sigma_{i=1}^{D}\lambda_i\boldsymbol{u}_i\boldsymbol{u}_i^\top \end{equation*}对于实对称矩阵\(\boldsymbol{\Sigma}\)可以作如下特征值分解:\(\boldsymbol{\Sigma} = \boldsymbol{Q}\boldsymbol{\Lambda}\boldsymbol{Q}^\top\), 其中\(\boldsymbol{Q}\)是以\(\boldsymbol{\Sigma}\)的特征向量为列向量的正交矩阵,而\(\boldsymbol{\Lambda}\)由对应特征值组成的对角矩阵。于是对于任意一个向量\(\boldsymbol{x}\),可以有如下推导:
\begin{equation*} \boldsymbol{\Sigma}\boldsymbol{x} = \boldsymbol{Q}\boldsymbol{\Lambda}\boldsymbol{Q}^{\top}\boldsymbol{x} = \boldsymbol{Q}\boldsymbol{\Lambda} \begin{bmatrix}\boldsymbol{u}_1^{\mathrm{T}}\boldsymbol{x}\\\vdots\\\boldsymbol{u_D^{\mathrm{T}}\boldsymbol{x}}\end{bmatrix} = \boldsymbol{Q}\begin{bmatrix}\lambda_1\boldsymbol{u}_1^{\mathrm{T}}\boldsymbol{x}\\\vdots\\\lambda_D\boldsymbol{u}_D^{\mathrm{T}}\boldsymbol{x}\end{bmatrix} = (\Sigma_{i=1}^D\lambda_i\boldsymbol{u}_i\boldsymbol{u}_i^{\mathrm{T}})\boldsymbol{x} \end{equation*}类似地可以推导出:
\begin{equation*} \boldsymbol{\Sigma}^{-1} = \Sigma_{i=1}^D\frac{1}{\lambda_i}\boldsymbol{u}_i\boldsymbol{u}_i^{\top} \end{equation*}将上式代入到二次项表达式中可以得到:
\begin{equation} \label{org2704260} \Delta^2 = \Sigma_{i=1}^D\frac{y_i^2}{\lambda_i} \end{equation}其中我们定义\(y_i = \boldsymbol{u}_i^{\top}(\boldsymbol{x} - \boldsymbol{\mu})\),进一步有\(\boldsymbol{y} = \boldsymbol{U}(\boldsymbol{x} - \boldsymbol{\mu})\),其中\(\boldsymbol{U}\)被定义为以\(\boldsymbol{u}_i^{\mathrm{T}}\)为行向量的矩阵。现在我们可以把\(\boldsymbol{y}\)看成新的坐标系,我们观察\eqref{org2704260},可以发现,如果协方差矩阵\(\boldsymbol{\Sigma}\)是正定(positive definite)的(即其所有特征值都是正的),那么在固定\(\Delta^2\)的情况下(即固定高斯分布密度值),在\(\boldsymbol{x}\)坐标系中就会是一个椭球,中心点为\(\boldsymbol{\mu}\),各个轴的方向为\(\boldsymbol{u}_i\),轴的长度为对应的特征值\(\lambda_i^{1/2}\)。
6.2. Singular vector decomposition
任意矩阵\(\boldsymbol{A} \in \mathbb{R}^{m \times n}\)都可以分解为: \(\boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}\),其 中 \(\boldsymbol{U} \in \mathbb{R}^{m \times m}\)和\(\boldsymbol{V} \in \mathbb{R}^{n \times n}\)都是正交矩阵(注意正交矩阵的定义:列向量标准 正交),此外\(\boldsymbol{\Sigma} \in \mathbb{R}^{m \times n}\)是一个 对角矩阵(注意对角矩阵的定义:行列号不等的元素均为零),对角元素被称为 \(\boldsymbol{A}\)的奇异值(singular values),记作\(\sigma_i\),且其中只 有前\(r = rank(\boldsymbol{A})\)个奇异值非零,通常按照从大到小排列: \(\sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > \sigma_{r+1} = \cdots = \sigma_{\min}(m,n) = 0\). 在这个基础上,我们来看下面两个式子:
\begin{equation*} \begin{aligned} \boldsymbol{A} \boldsymbol{A}^{\top} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}} (\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}})^{\mathrm{T}} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}} \boldsymbol{V} \boldsymbol{\Sigma}^{\mathrm{T}} \boldsymbol{U}^{\mathrm{T}} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{\Sigma}^{\mathrm{T}} \boldsymbol{U}^{\mathrm{T}}\\ \boldsymbol{A}^{\top} \boldsymbol{A} = (\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}})^{\mathrm{T}} \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}} = \boldsymbol{V} \boldsymbol{\Sigma}^{\mathrm{T}} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}} = \boldsymbol{V} \boldsymbol{\Sigma}^{\mathrm{T}} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}} \end{aligned} \end{equation*}由此可见,\(\boldsymbol{U}\)(左奇异矩阵)的列向量是矩阵 \(\boldsymbol{A}\boldsymbol{A}^{\top}\)的特征向量,而\(\boldsymbol{V}\)(右奇异矩 阵)的列向量是矩阵\(\boldsymbol{A}^{\top}\boldsymbol{A}\)的特征向量,而 \(\boldsymbol{A}\)的奇异值(即\(\boldsymbol{\Sigma}\)的对角元素)即为 \(\boldsymbol{A}\boldsymbol{A}^{\top}\)或\(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}\)的特征 值的平方根。
6.3. Dimensionality reduction
6.3.1. Principal component analysis
PCA是一种无监督的降维方法,也就是说它不需要数据有标签。它的基本思想是 给定一个数据矩阵,寻找一个或多个正交的方向使得映射后的数据方差 (variance)最大,直观理解为使降维后的数据尽量可分。
令\(\boldsymbol{X} \in \mathbb{R}^{n \times d}\)为数据矩阵,\(n\)个\(d\)维 数据点。不妨假设数据点列向量均值都为零(即使不是也可以通过列向量元素减 去所在列均值来达到这个效果) 2. 那么,将矩阵映射到单位向量\(\boldsymbol{v}\):
\begin{equation*} \frac{1}{n}\sum_{i=1}^n(\boldsymbol{x}_i^{\top}\boldsymbol{v})^2 = \frac{1}{n}\|\boldsymbol{X}\boldsymbol{v}\|^2 = \frac{1}{n}\boldsymbol{v}^{\mathrm{T}}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{v} \end{equation*}在此基础上,我们定义第一个载荷向量(first loading vector)为如下约束优化的解:
\begin{equation} \label{orgb7b548a} \begin{aligned} \boldsymbol{v}_1 = \operatorname*{arg\,max}_{\boldsymbol{v}} &\; \boldsymbol{v}^{\top}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{v} \\ \text{subject to} &\; \boldsymbol{v}^{\top}\boldsymbol{v} = 1 \end{aligned} \end{equation}其拉格朗日方程为:
\begin{equation*} \mathcal{L}(\boldsymbol{v}) = \boldsymbol{v}^{\top}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{v} - \lambda (\boldsymbol{v}^{\mathrm{T}}\boldsymbol{v} - 1) \end{equation*}令其导数为零:
\begin{equation*} \boldsymbol{0} = \nabla \mathcal{L}(\boldsymbol{v}_1) = 2 \boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{v}_1 - 2 \lambda \boldsymbol{v}_1 \end{equation*}于是有\(\boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{v}_1 = \lambda\boldsymbol{v}_1\),也就是说\(\boldsymbol{v}_1\)和\(\lambda\)即为 \(\boldsymbol{X}^{\top}\boldsymbol{X}\)的特征向量和特征值,我们在该式左右各乘 以\(\boldsymbol{v}_1^{\top}\),于是有:
\begin{equation*} \boldsymbol{v}_1^{\top}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{v}_1 = \boldsymbol{v}_1^{\mathrm{T}}(\lambda \boldsymbol{v}_1) = \lambda \boldsymbol{v}_1^{\mathrm{T}}\boldsymbol{v}_1 = \lambda \end{equation*}于是优化问题\eqref{orgb7b548a}的最大值即为\(\lambda\)的最大值,也就是有 \(\lambda=\lambda_{\max}(\boldsymbol{X}^{\top}\boldsymbol{X})\),即 \(\boldsymbol{X}^{\top}\boldsymbol{X}\)的最大特征值,而\(\boldsymbol{v}_1\)为该最 大特征值对应的特征向量。
按照上面的方法我们找到了第一主成分,接下来我们找更多的主成分,除 \(\boldsymbol{v}_1\)即第一主成分代表的映射方向外,其他主成分代表的方向也需 要让数据方差尽量大,同时,为了减少与已有主成分的冗余,这些主成分需要与 现有的主成分方向保持正交。据此,我们定义第\(k\)个载荷向量 \(\boldsymbol{v}_k\)为下列有约束最优化问题的解:
\begin{equation*} \begin{aligned} \boldsymbol{v}_k = \operatorname*{arg\,max}_{\boldsymbol{v}} &\; \boldsymbol{v}^{\top}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{v} \\ \text{subject to} &\; \boldsymbol{v}^{\top}\boldsymbol{v} = 1; \\ &\; \boldsymbol{v}^{\top}\boldsymbol{v}_i = 0, i = 1,2,\cdots, k-1 \end{aligned} \end{equation*}这里,我们略去证明过程(通过归纳假设证明),只给出结论: \(\boldsymbol{v}_k\)即为\(\boldsymbol{X}^{\top}\boldsymbol{X}\)第\(k\)大的特征值对 应的单位特征向量。
至此,我们发现达标映射方向的载荷向量即为 \(\boldsymbol{X}^{\top}\boldsymbol{X}\)的正交的特征向量,即矩阵\(\boldsymbol{X}\) 的右奇异向量。完整的PCA降维可以表述如下:
\begin{equation*} \boldsymbol{Z}_k = \boldsymbol{X} \boldsymbol{V}_k, \; \boldsymbol{X} \in \mathbb{R}^{n \times d}, \, \boldsymbol{V}_k \in \mathbb{R}^{d \times k} \end{equation*}表示从\(n\)维降到\(k\)维,\(\boldsymbol{V}_k\)的列向量是\(X\)的前\(k\)个载 荷向量,即为其前\(k\)大的奇异值对应的右奇异向量。
6.3.2. Canonical correlation analysis
PCA降维有两大缺陷:
- 对于某些方差本身很大然而却对实际分类并不起太大作用的特征(试想某个 特征包含方差很大的噪声),PCA并不能很好的处理,因为它是一个无监督的 方法。
- PCA结果与特征的单位或尺度变化有关。
典型相关分析实际上是一种基于皮尔逊相关系数的分析两组多元数据相关性的方 法。如果从回归的角度上来理解,那么CCA就可以把输入数据矩阵降到一维,然 后分析与输出序列的相关性;如果从多分类的角度来理解,假设将\(n\)个样本 分成\(k\)类,那么输出的矩阵就是\(\mathbb{R}^{n \times k}\),每一行有且 仅有一个位置为1,其它位置为零,那么CCA就可以把输入数据矩阵降到\(k\)维。
CCA与PCA相比,PCA优化的是最大化数据本身的方差,而CCA优化的是最大化数据 与标签之间的相关系数,比较一下他们的形式 3:
\begin{equation*} \begin{aligned} \text{PCA:} &\quad \boldsymbol{v}_1 = \operatorname*{arg\,max}_{\boldsymbol{v}} \text{Var}(\boldsymbol{X}\boldsymbol{v}); \;\; \boldsymbol{X} \in \mathbb{R}^{n \times d}, \boldsymbol{v} \in \mathbb{R}^{k} \\ \text{CCA:} &\quad \boldsymbol{u}_1, \boldsymbol{v}_1 = \operatorname*{arg\,max}_{\boldsymbol{u}, \boldsymbol{v}} \rho(\boldsymbol{X}\boldsymbol{u}, \boldsymbol{Y}\boldsymbol{v}); \;\; \boldsymbol{X} \in \mathbb{R}^{n \times p}, \boldsymbol{Y}\in\mathbb{R}^{n \times q}, \boldsymbol{u}\in\mathbb{R}^{p}, \boldsymbol{v}\in\mathbb{R}^{q} \end{aligned} \end{equation*}6.4. Regression
机器学习的目标是要从数据中提取它们的关系,在回归任务中,这种关系被写作 \(y=f(\boldsymbol{x})\),即给定一个\(d\)维的样本数据\(\boldsymbol{x} \in \mathbb{R}^d\),输出某个量化值\(y\),真实的函数\(f\)是未知的,所以我们 需要一个假设函数\(\hat{y} = h(\boldsymbol{x})\)以尽可能地使假设 (hypothesis)\(\hat{y}\)贴近真实的输出值\(y\)。当然,假设函数可以是任 意的(比如可以用一个针对输入输出值的if-else的函数,不过这样泛化能力会 很弱),求这样的任意函数是非常棘手的,所以为了解决这个问题,回归分析的 思想是采用参数模型(parametric model),即把假设函数限制到只允许某些函 数的空间(hypothesis class),用一个有限维度的参数\(\boldsymbol{w} \in \mathbb{R}^d\)来做拟合,即有:
\begin{equation*} h_{\boldsymbol{w}}(\boldsymbol{x}) = g(\boldsymbol{x}, \boldsymbol{w}) \end{equation*}剩下的就是定义损失函数(lost function)来求使损失函数最小的 \(\boldsymbol{w}^{\ast}\).
6.4.1. Ordinary least squares
给定数据表示为\(\boldsymbol{x} \in \mathbb{R}^{n \times d}\),即特征数为 \(d\)的\(n\)个样本(通常样本数大于特征数\(n \geq d\)),参数向量为 \(\boldsymbol{w} \in \mathbb{R}^d\),标签向量为\(\boldsymbol{y} \in \mathbb{R}^n\),输出函数定义\(\boldsymbol{y} = \boldsymbol{X}\boldsymbol{w}\),根 据最小二乘法给出损失函数(Lost function):
\begin{equation*} L(\boldsymbol{w}) = \|\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y}\|^2_2 \end{equation*}目标是求得使损失函数达到最小的\(\boldsymbol{w}^{\ast}\):
\begin{equation*} \boldsymbol{w}^{\ast} = \operatorname*{arg\,min}_{\boldsymbol{w}}L(\boldsymbol{w}) \end{equation*}- Approach 1: vector calculus
我们把损失函数看成是一种投影\(L: \mathbb{R}^2 \rightarrow \mathbb{R}\), 如果它是连续可微的,那么就存在局部最优的一个\(\boldsymbol{w}^{\ast}\)满足 \(\nabla L(\boldsymbol{w}^{\ast}) = \boldsymbol{0}\),为了求得这个局部最优点:
\begin{equation*} \begin{split} L(\boldsymbol{w}) &= \|\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y}\|^2_2 \\ &= (\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y})^{\top}(\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y}) \\ &= (\boldsymbol{X}\boldsymbol{w})^{\top}\boldsymbol{X}\boldsymbol{w} - (\boldsymbol{X}\boldsymbol{w})^{\mathrm{T}}\boldsymbol{y} - \boldsymbol{y}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{w} + \boldsymbol{y}^{\mathrm{T}}\boldsymbol{y} \\ &= \boldsymbol{w}^{\top}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{w} - 2\boldsymbol{w}^{\mathrm{T}}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} + \boldsymbol{y}^{\mathrm{T}}\boldsymbol{y} \end{split} \end{equation*}对其求微分:
\begin{equation*} \begin{split} \nabla L(\boldsymbol{w}) &= \nabla_{\boldsymbol{w}}(\boldsymbol{w}^{\top}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{w} - 2\boldsymbol{w}^{\mathrm{T}}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} + \boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}) \\ &= \nabla_{\boldsymbol{w}}(\boldsymbol{w}^{\top}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{w}) - 2\nabla_{\boldsymbol{w}}(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{y}) + \nabla_{\boldsymbol{w}}(\boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}) \\ &= 2\boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{w} - 2\boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} \end{split} \end{equation*}注意这里的\(\boldsymbol{X}^{\top}\boldsymbol{X}\)是对称矩阵,所以其二次型 (quadratic form)的微分很容易求得。令\(\nabla L(\boldsymbol{w}) = 0\),得 到最优点\(\boldsymbol{w}^{\ast}\)满足:
\begin{equation*} \boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{w}^{\ast} = \boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} \end{equation*}到这里,如果\(\boldsymbol{X} \in \mathbb{R}^{n \times d}\)是列满秩的(因为 我们假设\(n \geq d\),所以列满秩的含义其实就是列向量线性无关),那么可 以推出\(\boldsymbol{X}^{\top}\boldsymbol{X} \in \mathbb{R}^{d \times d}\)是满 秩的,那么我们就可以得到最优点:
\begin{equation*} \boldsymbol{w}^{\ast} = (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} \end{equation*}该最优点能成为全局最小值点(因为微分为零的点可能是局部最优点,也可能是 最大值点,也可能是鞍点)是由目标函数\(L\)的凸(convex)来保证的,为了 证明\(L\)的凸性,可以计算它的海森矩阵(Hessian):
\begin{equation*} \nabla^2 L(\boldsymbol{w}) = 2\boldsymbol{X}^{\top}\boldsymbol{X} \end{equation*}由于:
\begin{equation*} \forall \boldsymbol{w}, \boldsymbol{w}^{\top}(2\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X})\boldsymbol{w} = 2(\boldsymbol{X}\boldsymbol{w})^{\mathrm{T}}\boldsymbol{X}\boldsymbol{w} = 2\|\boldsymbol{X}\boldsymbol{w}\|^2_2 \geq 0 \end{equation*}也就是说\(L\)的海森矩阵是半正定的(positive semi-definite),这就证明 了\(L\)是凸的,也就证明了局部极值点\(\boldsymbol{w}^{\ast}\)就是全局最小值 点。注意,因为海森矩阵是半正定而非正定,所以一旦海森矩阵存在零特征值, 那么\(\boldsymbol{X}^{\top}\boldsymbol{X}\)就不可逆,在这种情况下,不代表全局 最优解(最小值)不存在,\(\boldsymbol{X}^{\top}\boldsymbol{X} \boldsymbol{w}= \boldsymbol{X}^{\top}\boldsymbol{y}\)的解总是存在的,只不过只有当海森矩阵为正 定的时候这个解才是唯一的,如果是半正定的,那么解就有无穷多个。
- Approach 2: Orthogonal projection
我们先把最小二乘放一放,来看一下正交投影(orthogonal projections)。
如果\(S\)是一个内积空间(inner product space)\(V\)的子空间,那么对于\(\forall \boldsymbol{v} \in V\),总可以有唯一的分解形式:\(\boldsymbol{v} = \boldsymbol{v}_S + \boldsymbol{v}_{\perp}\),其中\(\boldsymbol{v}_S \in S\),\(\boldsymbol{v}_{\perp} \in S^{\perp}\).
基于以上分解,可以定义内积空间\(V\)在其子空间\(S\)上的正交投影:\(P_S\),它有一个重要性质:
\begin{equation*} \|\boldsymbol{v} - \boldsymbol{s}\| \geq \|\boldsymbol{v} - P_S\boldsymbol{v}\|, \, \forall \boldsymbol{s} \in S \end{equation*}等号只在\(\boldsymbol{s} = P_S \boldsymbol{v}\)的时候取得,即有:
\begin{equation} \label{org3e141c2} P_S\boldsymbol{v} = \operatorname*{arg\,min}_{\boldsymbol{s} \in S}\|\boldsymbol{v} - \boldsymbol{s}\| \end{equation}该性质证明如下:
根据毕达哥拉斯定理(Pythagorean theorem),有
\begin{equation*} \|\boldsymbol{v} - \boldsymbol{s}\|^2 = \|\boldsymbol{v} - P_S\boldsymbol{v} + P_S\boldsymbol{v} - \boldsymbol{s}\|^2 = \|\boldsymbol{v} - P_S\boldsymbol{v}\|^2 + \|P_S\boldsymbol{v} - \boldsymbol{s}\|^2 \geq \|\boldsymbol{v} - P_S\boldsymbol{v}\|^2 \end{equation*}等号只在\(\boldsymbol{s} = P_S\boldsymbol{v}\)时取得。两边求平方根即得到\(\|\boldsymbol{v} - \boldsymbol{s}\| \geq \|\boldsymbol{v} - P_S\boldsymbol{v}\|\).
我们回到最小二乘问题:
\begin{equation*} \boldsymbol{w}^{\ast} = \operatorname*{arg\,min}_{\boldsymbol{w}}\|\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y}\|^2_2 \end{equation*}稍做变换:
\begin{equation*} \begin{split} \boldsymbol{w}^{\ast} &= \operatorname*{arg\,min}_{\boldsymbol{w} \in \mathbb{R}^d} \|\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y}\|^2_2 \\ &= \operatorname*{arg\,min}_{\boldsymbol{X}\boldsymbol{w} \in range(\boldsymbol{X})}\|\boldsymbol{y} - \boldsymbol{X}\boldsymbol{w}\| \end{split} \end{equation*}结合等式\eqref{org3e141c2},上式可以看作\(\boldsymbol{y}\)所在空间在\(\boldsymbol{X}\boldsymbol{w}\)所在空间(即\(range(\boldsymbol{X})\))上的正交投影,考虑等号成立条件,得到:
\begin{equation*} \boldsymbol{X}\boldsymbol{w}^{\ast} = P_{range(\boldsymbol{X})}\boldsymbol{y} \end{equation*}再结合定理1,可以推出\(\boldsymbol{y} - P_{range(\boldsymbol{X})} \boldsymbol{y} \perp range(\boldsymbol{X})\),也就是\(\boldsymbol{y} - \boldsymbol{X}\boldsymbol{w}^{\ast} \in null(\boldsymbol{X}^{\top})\). 4 即可以推出:
\begin{equation*} \begin{aligned} \boldsymbol{X}^{\top} (\boldsymbol{y} - \boldsymbol{X}\boldsymbol{w}^{\ast}) = \boldsymbol{0} \\ \boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{w}^{\ast} = \boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} \end{aligned} \end{equation*}
6.4.2. Ridge regression
最小二乘法的解析解要求\(\boldsymbol{X}^{\top}\boldsymbol{X}\)可逆,其等价的条 件是\(\boldsymbol{X}\)满秩,如果其中有两个列向量线性相关,即有两个特征在数 据集上有相同的表现,那么就会出现\(\boldsymbol{X}\)是奇异矩阵的情况,也就是 说\(\boldsymbol{X}^{\top}\boldsymbol{X}\)不可逆,也就无法用最小二乘来求解了。 即使\(\boldsymbol{X}\)中没有完全线性相关的列向量,如果有列向量近似共线 (close to collinear),那么也会出现问题,列向量近似共线导致其特征值很 小,考虑\(\boldsymbol{X}\)的SVD分解:
\begin{equation*} \boldsymbol{X} = \boldsymbol{U} \begin{bmatrix} \boldsymbol{\Sigma}_d \\ \boldsymbol{0} \end{bmatrix} \boldsymbol{V}^{\top} \end{equation*}其中(\(d\)是\(\boldsymbol{X}\)的秩),那么有:
\begin{equation*} \begin{split} (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1} &= (\boldsymbol{V}\begin{bmatrix}\boldsymbol{\Sigma}_b & \boldsymbol{0}\end{bmatrix} \boldsymbol{U}^{\mathrm{T}}\boldsymbol{U}\begin{bmatrix}\boldsymbol{\Sigma}_d \\ \boldsymbol{0}\end{bmatrix} \boldsymbol{V}^{\mathrm{T}})^{-1} \\ &= (\boldsymbol{V}\begin{bmatrix}\boldsymbol{\Sigma}_d & \boldsymbol{0}\end{bmatrix} \boldsymbol{I} \begin{bmatrix}\boldsymbol{\Sigma}_d \\ \boldsymbol{0}\end{bmatrix} \boldsymbol{V}^{\top})^{-1} \\ &= (\boldsymbol{V} \boldsymbol{\Sigma}^2_d \boldsymbol{V}^{\top})^{-1} \\ &= (\boldsymbol{V}^{\top})^{-1}(\boldsymbol{\Sigma}^2_d)^{-1}\boldsymbol{V}^{-1} \\ &= \boldsymbol{V}\boldsymbol{\Sigma}^{-2}_d\boldsymbol{V}^{\top} \end{split} \end{equation*}一旦某个特征值很小,那么会导致最后的参数向量\(\boldsymbol{w}^{\ast}\)中存 在很大的元素,也就会带来数值不稳定。这个现象还可以从参数向量的期望和方 差的角度来解释:
\begin{equation*} \begin{aligned} \mathbb{E}(\boldsymbol{w}^{\ast}) &= \mathbb{E}[(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{Y}] \\ &= (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\mathrm{T}}\mathbb{E}(\boldsymbol{Y}) \\ &= (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{w} \\ &= \boldsymbol{w} \\ Cov(\boldsymbol{w}^{\ast}) &= \mathbb{E}\{[\boldsymbol{w}^{\ast} - \mathbb{E}(\boldsymbol{w}^{\ast})][\boldsymbol{w}^{\ast} - \mathbb{E}(\boldsymbol{w}^{\ast})]^{\top}\} \\ &= \mathbb{E}\{[(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{Y} - \boldsymbol{w}][(\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X})^{-1}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{Y} - \boldsymbol{w}]^{\mathrm{T}}\} \\ &= (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\mathrm{T}}\mathbb{E}(\boldsymbol{Y}\boldsymbol{Y}^{\mathrm{T}})\boldsymbol{X}(\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X})^{-1} - \boldsymbol{w}\boldsymbol{w}^{\mathrm{T}} \\ &= (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\mathrm{T}}(\boldsymbol{X}\boldsymbol{w}\boldsymbol{w}^{\mathrm{T}}\boldsymbol{X}^{\mathrm{T}} + \boldsymbol{\Sigma})\boldsymbol{X}(\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X})^{-1} - \boldsymbol{w}\boldsymbol{w}^{\mathrm{T}} \\ &= \boldsymbol{w}\boldsymbol{w}^{\top} + {\sigma}^2(\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X})^{-1} - \boldsymbol{w}\boldsymbol{w}^{\mathrm{T}} \\ &= {\sigma}^2(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1} \end{aligned} \end{equation*}前面说到的\((\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\)中有元素值很大,导致协 方差矩阵中有很大的元素,这可以解释为该模型的variance很大,或者说过拟合 (overfitting)、泛化性差、对未知的新数据不稳定、对原有数据上的轻微扰 动敏感。
为了解决这个问题,可以在损失函数中加入罚项(penalty term),防止 \(\boldsymbol{w}\)中的元素变得过大,这里采用一个常量\(\lambda > 0\):
\begin{equation*} \begin{split} L(\boldsymbol{w}) &= \|\boldsymbol{X}\boldsymbol{w} - \boldsymbol{y}\|^2_2 + \lambda\|\boldsymbol{w}\|^2_2 \\ &= \boldsymbol{w}^{\top}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{w} - 2 \boldsymbol{w}^{\mathrm{T}}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} + \boldsymbol{y}^{\mathrm{T}}\boldsymbol{y} + \lambda\boldsymbol{w}^{\mathrm{T}}\boldsymbol{w} \end{split} \end{equation*}求导数为零的极值点:
\begin{equation*} \begin{aligned} \nabla_{\boldsymbol{w}} L(\boldsymbol{w}) &= \boldsymbol{0} \\ 2\boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{w} - 2\boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} + 2 \lambda \boldsymbol{w} &= \boldsymbol{0} \\ (\boldsymbol{X}^{\top}\boldsymbol{X} + \lambda \boldsymbol{I})\boldsymbol{w} &= \boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} \\ \boldsymbol{w}^{\ast} = (\boldsymbol{X}^{\top}\boldsymbol{X} + \lambda\boldsymbol{I})^{-1}\boldsymbol{X}^{\mathrm{T}}\boldsymbol{y} \end{aligned} \end{equation*}求得的局部极值点即为全局最小点,因为目标函数是强凸的(strongly convex), 为证明它是强凸的,可以用目标函数的海森矩阵:
\begin{equation*} \nabla^2L(\boldsymbol{w}) = 2\boldsymbol{X}^{\top}\boldsymbol{X} + 2\lambda\boldsymbol{I} \end{equation*}可以证明它是正定的(positive definite):
\begin{equation*} \forall \boldsymbol{w} \neq \boldsymbol{0}, \, \boldsymbol{w}^{\top}(\boldsymbol{X}^{\mathrm{T}}\boldsymbol{X} + \lambda\boldsymbol{I})\boldsymbol{w} = (\boldsymbol{X}\boldsymbol{w})^{\mathrm{T}}\boldsymbol{X}\boldsymbol{w} + \lambda\boldsymbol{w}^{\mathrm{T}}\boldsymbol{w} = \|\boldsymbol{X}\boldsymbol{w}\|^2_2 + \lambda\|\boldsymbol{w}\|^2_2 > 0 \end{equation*}故而目标函数\(L\)是强凸的,所以导数为零处的局部极值点即为全局最小值点。 跟最小二乘法中的目标函数不一样,强凸的目标函数意味着最优解是唯一的。所 以不管\(\boldsymbol{X}\)是不是满秩的,利用\(\boldsymbol{X}\)的SVD分解,总有:
\begin{equation*} \begin{split} \boldsymbol{X}^{\top}\boldsymbol{X} + \lambda\boldsymbol{I} &= \boldsymbol{V} \begin{bmatrix} \boldsymbol{\Sigma}_r & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{bmatrix} \boldsymbol{U}^{\top}\boldsymbol{U} \begin{bmatrix} \boldsymbol{\Sigma}_r & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{bmatrix} \boldsymbol{V}^{\top} + \lambda\boldsymbol{I}) \\ &= \boldsymbol{V} \begin{bmatrix} \boldsymbol{\Sigma}_r^2 & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{bmatrix} \boldsymbol{v}^{\top} + \lambda\boldsymbol{I} \\ &= \boldsymbol{V} \begin{bmatrix} \boldsymbol{\Sigma}_r^2 & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{bmatrix} \boldsymbol{V}^{\top} + \boldsymbol{V}(\lambda\boldsymbol{I})\boldsymbol{V}^{\mathrm{T}} \\ &= \boldsymbol{V}( \begin{bmatrix} \boldsymbol{\Sigma}_r^2 & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{bmatrix} + \lambda\boldsymbol{I})\boldsymbol{V}^{\top} \\ &= \boldsymbol{V} \begin{bmatrix} \boldsymbol{\Sigma}_r^2 + \lambda\boldsymbol{I} & \boldsymbol{0} \\ \boldsymbol{0} & \lambda\boldsymbol{I} \end{bmatrix} \boldsymbol{V}^{\top} \end{split} \end{equation*}所以\(\boldsymbol{X}^{\top}\boldsymbol{X} + \lambda\boldsymbol{I}\)是满秩的,一方 面可以保证其可逆,另一方面,其奇异值元素值至少为\(\lambda\),从而避免 了OLS中可能出现的数值不稳定性。
6.4.3. Maximum likelihood estimation
最大似然估计(MLE)的目标是要寻找一个假设模型使由该模型产生现有数据的 概率最大 5. 设概率模型的参数为 \(\boldsymbol{\theta}\),则有:
\begin{equation*} \hat{\boldsymbol{\theta}}_{\text{MLE}} = \operatorname*{arg\,max}_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta}; \mathcal{D}) = \operatorname*{arg\,max}_{\boldsymbol{\theta}} p(\text{data} = \mathcal{D} \mid \text{true\;model} = h_{\boldsymbol{\theta}}) \end{equation*}用输入输出向量来替换数据集\(\mathcal{D}\)的表示,注意\(\mathcal{L}(\boldsymbol{\theta}; \boldsymbol{X}, \boldsymbol{y})\)表示由\(\boldsymbol{X}\)和\(\boldsymbol{y}\)参数化关于\(\boldsymbol{\theta}\)的函数:
\begin{equation*} \hat{\boldsymbol{\theta}}_{\text{MLE}} = \operatorname*{arg\,max}_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}; \boldsymbol{X}, \boldsymbol{y}) = \operatorname*{arg\,max}_{\boldsymbol{\theta}} p(y_1, \cdots, y_n \mid \boldsymbol{x}_1, \cdots, \boldsymbol{x}_n, \boldsymbol{\theta}) \end{equation*}由于\(\log(x)\)是单调增函数,故而可以进一步写成:
\begin{equation*} \hat{\boldsymbol{\theta}}_{\text{MLE}} = \operatorname*{arg\,max}_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}; \boldsymbol{X}, \boldsymbol{y}) = \operatorname*{arg\,max}_{\boldsymbol{\theta}}\log\mathcal{L}(\boldsymbol{\theta}; \boldsymbol{X}, \boldsymbol{y}) = \operatorname*{arg\,max}_{\boldsymbol{\theta}}\ell(\boldsymbol{\theta}; \boldsymbol{X}, \boldsymbol{y}) \end{equation*}假设每一个\(\boldsymbol{y}_i\)都来自独立同分布的高斯分布\(Y_i \sim \mathcal{N}(h_{\boldsymbol{\theta}}(\boldsymbol{x}_i), \sigma^2)\),所以有:
\begin{equation*} \ell(\boldsymbol{\theta}; \boldsymbol{X}, \boldsymbol{y}) = \log p(y_1, \cdots, y_n \mid \boldsymbol{x}_1, \cdots, \boldsymbol{x}_n, \boldsymbol{\theta}) = \log \prod_{i=1}^n p(y_i \mid \boldsymbol{x}_i, \boldsymbol{\theta}) = \sum_{i=1}^n \log[p(y_i \mid \boldsymbol{x}_i, \boldsymbol{\theta})] \end{equation*}考虑高斯分布的概率密度函数,从而有:
\begin{equation*} \begin{split} \hat{\boldsymbol{\theta}}_{\text{MLE}} &= \operatorname*{arg\,max}_{\boldsymbol{\theta}} \ell(\boldsymbol{\theta}; \boldsymbol{X}, \boldsymbol{y}) \\ &= \operatorname*{arg\,max}_{\boldsymbol{\theta}}\sum_{i=1}^n \log[p(y_i \mid \boldsymbol{x}_i, \boldsymbol{\theta})] \\ &= \operatorname*{arg\,max}_{\boldsymbol{\theta}} -(\sum_{i=1}^n\frac{(y_i - h_{\boldsymbol{\theta}}(\boldsymbol{x}_i))^2}{2\sigma^2}) - n\log\sqrt{2\pi}\sigma \\ &= \operatorname*{arg\,min}_{\boldsymbol{\theta}}(\sum_{i=1}^n\frac{(y_i - h_{\boldsymbol{\theta}}(\boldsymbol{x}_i))^2}{2\sigma^2}) + n \log\sqrt{2\pi}\sigma \\ &= \operatorname*{arg\,min}_{\boldsymbol{\theta}}\sum_{i=1}^n(y_i - h_{\boldsymbol{\theta}}(\boldsymbol{x}_i))^2 \end{split} \end{equation*}考虑回归的情况,有\(h_{\boldsymbol{\theta}}(\boldsymbol{x}_i) = \boldsymbol{x}_i^{\top}\boldsymbol{\theta}\),那么最大似然估计可以写成:
\begin{equation*} \hat{\boldsymbol{\theta}}_{\text{MLE}} = \operatorname*{arg\,min}_{\boldsymbol{\theta} \in \mathbb{R}^d} \sum_{i=1}^n(y_i - \boldsymbol{x}_i^{\top}\boldsymbol{\theta})^2 \end{equation*}此即最小二乘之问题,至此,可以发现OLS和MLE其实本质上是统一的。
6.4.4. Maximum a posteriori
最大后验估计(MAP)的目标是要寻找一个假设模型,使现有数据符合该模型的 概率最大 6:
\begin{equation*} \hat{\boldsymbol{\theta}}_{\text{MAP}} = \operatorname*{arg\,max}_{\boldsymbol{\theta}}p(\text{true\;model} = h_{\boldsymbol{\theta}} \mid \text{data} = \mathcal{D}) \end{equation*}直接计算这个后验概率通常很难,故而我们利用贝叶斯规则(Bayes' Rule):
\begin{equation*} \begin{split} \hat{\boldsymbol{\theta}}_{\text{MAP}} &= \operatorname*{arg\,max}_{\boldsymbol{\theta}} p (\text{true\;model} = h_{\boldsymbol{\theta}} \mid \text{data} = \mathcal{D}) \\ &= \operatorname*{arg\,max}_{\boldsymbol{\theta}} \frac{p(\text{data} = \mathcal{D} \mid \text{true\;model} = h_{\boldsymbol{\theta}}) \cdot p(\text{true\;model} = h_{\boldsymbol{\theta}})}{p(\text{data} = \mathcal{D})} \\ &= \operatorname*{arg\,max}_{\boldsymbol{\theta}} p(\text{data} = \mathcal{D} \mid \text{true\;model} = h_{\boldsymbol{\theta}}) \cdot p(\text{true\;model} = h_{\boldsymbol{\theta}}) \\ &= \operatorname*{arg\,max}_{\boldsymbol{\theta}} \log p(\text{data} = \mathcal{D} \mid \text{true\;model} = h_{\boldsymbol{\theta}}) + \log p(\text{true\;model} = h_{\boldsymbol{\theta}}) \\ &= \operatorname*{arg\,min}_{\boldsymbol{\theta}} -\log p(\text{data} = \mathcal{D} \mid \text{true\;model} = h_{\boldsymbol{\theta}}) - \log p(\text{true\;model} = h_{\boldsymbol{\theta}}) \end{split} \end{equation*}可以发现,MAP的优化目标和MLE很像(前半部分就是MLE),只不过加上了 \(p(\text{true\;model}=h_{\boldsymbol{\theta}})\),即先验(prior),考 虑先验的效果是让模型本身之间有偏见(与数据集无关),而MLE其实是MAP的 特例,它把所有模型都同等看待。具体地有:
\begin{equation*} \hat{\boldsymbol{\theta}}_{\text{MAP}} = \operatorname*{arg\,min}_{\boldsymbol{\theta}} -(\sum_{i=1}^n \log[p(y_i \mid \boldsymbol{x}_i, \boldsymbol{\theta})]) - \log[p(\boldsymbol{\theta})] \end{equation*}考虑模型参数服从独立同分布的高斯分布:\(\Theta_j \stackrel{iid}{\sim} \mathcal{N}(\theta_{j_0}, \sigma_h^2)\),于是有:
\begin{equation*} \begin{split} \hat{\boldsymbol{\theta}}_{\text{MAP}} &= \operatorname*{arg\,min}_{\boldsymbol{\theta}}(\frac{\sum_{i=1}^n(y_i - h_{\boldsymbol{\theta}}(\boldsymbol{x}_i))^2}{2\sigma^2}) + (\frac{\sum_{j=1}^d(\theta_j - \theta_{j_0})^2}{2\sigma_h^2}) \\ &= \operatorname*{arg\,min}_{\boldsymbol{\theta}}(\sum_{i=1}^2(y_i - h_{\boldsymbol{\theta}}(\boldsymbol{x}_i))^2) + \frac{\sigma^2}{\sigma_h^2}(\sum_{j=1}^d(\theta_j - \theta_{j_0})^2) \end{split} \end{equation*}当\(\theta_{j_0}=0\),从线性回归的角度考虑,再利用\(h_{\boldsymbol{\theta}}(\boldsymbol{x}) = \boldsymbol{\theta}^{\top}\boldsymbol{x}\)写成:
\begin{equation*} \hat{\boldsymbol{\theta}}_{\text{MAP}} = \operatorname*{arg\,min}_{\boldsymbol{\theta} \in \mathbb{R}^d}\sum_{i=1}^n(y_i - \boldsymbol{x}_i^{\top}\boldsymbol{\theta})^2 + \frac{\sigma^2}{\sigma^2_h}\sum_{j=1}^d\theta^2_j \end{equation*}可以发现,MAP的优化目标与岭回归问题是统一的,岭回归中的参数\(\lambda = \frac{\sigma^2}{\sigma^2_h}\)。
6.5. Classification
6.5.1. Naive Bayes
用\(C\)表示分类类别:\(dom(C)=\{c_1, c_2, \cdots, c_n\}\),用\(A\)表示观测的特征:\(dom(A)=\{a_1, a_2, \cdots, a_m\}\)。对于一个待分类的样本,实际上就是一种特征的组合,那么可以由贝叶斯规则算出在这样的特征组合的情况下属于每个分类的概率:
\begin{equation*} P(C=c_i \mid A_1=a_1,A_2=a_2,\cdots,A_m=a_m) = \frac{P(A_1=a_1,A_2=a_2,\cdots,A_m=a_m \mid C= c_i) P(C=c_i)}{P(A_1=a_1, A_2=a_2, \cdots, A_m=a_m)} \end{equation*}但是,问题是分子上面的那个条件概率比较麻烦,因为如果特征一多,那么要将所有特征组合都穷尽一遍。所以就有了朴素贝叶斯来简化计算,朴素贝叶斯的“朴素”之处在于它假设特征之间相互独立,所以上式中分子的条件概率可以写成:
\begin{equation*} P(A_1=a_1,A_2=a_2,\cdots,A_m=a_m \mid C= c_i) = \prod_{j=1}^mP(A_j=a_j \mid C=c_i) \end{equation*}然后再代到上面的公式就简单了。另外,对于连续数值型特征,需要用概率密度函数来计算概率。
6.5.2. Support Vector Machines
考虑二分类问题,样本用向量\(\boldsymbol{x}\)表示,类比为\(\boldsymbol{y}\in \{-1,1\}\),SVM的核心思想是:寻找一个超平面,定义一个“距离”,计算所有数据点到该平面的“距离”,使得其中最小的“距离”达到最大。
- 从函数间隔到几何间隔
首先考虑线性可分的情况。定义带有参数\(\boldsymbol{w},b\)的超平面\(\boldsymbol{w}^{\top}\boldsymbol{x} + b\),给定第\(i\)个测试样本\((\boldsymbol{x}^{(i)}, y^{(i)})\),那么其到该平面到函数间隔(Functional Margin)为:
\[ \hat{\gamma}^{(i)} = y^{(i)}(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)} + b) \]
可以发现,如果对超平面对参数\(\boldsymbol{w}, b\)等比例地放大缩小,其实际作用不变(即不影响分类结果),但是函数间隔会随之变化,所以用如此定义的函数来衡量样本点到某分类超平面的“距离”并不可靠。因此,考虑将超平面等式归一化,因此就有了:
\[ \gamma^{(i)} = y^{(i)}((\frac{\boldsymbol{w}}{\left\|\boldsymbol{w}\right\|})^{\top}\boldsymbol{x}^{(i)} + \frac{b}{\left\|\boldsymbol{w}\right\|}) \]
这个经归一化后的函数间隔被成为几何间隔(Geometric Margin),其可以很好地衡量样本点到某分类超平面到“距离”。
- 最优化问题
有了对样本点到超平面的“距离”的定义(可以理解成某样本点被正确分类的信心),就可以通过使离分类超平面最近的点到分类超平面的距离最大来求得一个最佳的分类超平面,于是就有了下面的最优化问题:
\begin{equation*} \begin{aligned} \max_{\gamma, \boldsymbol{w}, b} \;& \gamma \\ \text{s.t.} \;& y^{(i)}(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)} + b) \geq \gamma , \; i = 1,\dots, m \\ \;& \left\|\boldsymbol{w}\right\| = 1. \end{aligned} \end{equation*}再进一步转化(个人感觉从归一化函数间隔的角度上来理解的话可以直接得到下面的形式):
\begin{equation*} \begin{aligned} \max_{\hat{\gamma}, \boldsymbol{w}, b} \;& \frac{\hat{\gamma}}{\left\|\boldsymbol{w}\right\|} \\ \text{s.t.} \;& y^{(i)}(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)} + b) \geq \hat{\gamma}, \; i = 1, \dots, m. \end{aligned} \end{equation*}由于函数间隔可以任意缩放而不影响结果,因此不妨设\(\hat{\gamma} = 1\),则优化目标变为了\(\max_{\boldsymbol{w}, b}\,\frac{1}{\left\|\boldsymbol{w}\right\|}\),为方便后续求解,一般写成如下形式:
\begin{equation*} \begin{aligned} \min_{\boldsymbol{w}, b} \;& \frac{1}{2}{\left\|\boldsymbol{w}\right\|}^2 \\ \text{s.t.} \;& y^{(i)}(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)} + b) \geq 1, \; i = 1,\dots,m. \end{aligned} \end{equation*}可以证明,该最优化问题的解是存在且唯一的。
- 松弛变量
由于在实际情况下样本可能无法做到线性可分,于是便引入了松弛变量(slack variables),其思想即是允许某些点到分类超平面的距离小于最优的分类间隔(甚至误分类),具体的优化问题可以表示成:
\begin{equation*} \begin{aligned} \min_{\boldsymbol{w}, b} \;& \frac{1}{2}{\left\|\boldsymbol{w}\right\|}^2 + C\Sigma_{i=1}^m \xi^{(i)} \\ \text{s.t.} \;& y^{(i)}(\boldsymbol{w}^{\top}\boldsymbol{x}^{(i)} + b) \geq 1 - \xi^{(i)}, \; \xi^{(i)} \geq 0. \end{aligned} \end{equation*}其中\(\xi^{(i)}\geq 0\)即松弛变量,其允许某些样本点不满足严格的间隔约束(此时\(0 \leq \xi^{(i)} \leq 1\))或被误分类(此时\(\xi^{(i)} > 1\))。而参数\(C > 0\)用于控制“最大化间隔”与“最小化松弛量”之间的权重。
- 核函数
除了采用线性分类器(即由线性函数定义的分类超平面),SVM还可以通过把数据点映射到高维空间以得到在原始空间中的非线性分类器。而不管在何种空间,我们定义分类器需要的都是点与面的距离而不是具体的映射函数,前者可以通过空间中的点积求得。我们定义从原始空间\(\mathcal{X}\)到特征空间\(\mathcal{F}\)的非线性映射\(\phi: \mathcal{X} \to \mathcal{F}\),于是可以定义核函数(kernel function)以接收原始空间中的点为输入来计算其在特征空间中的点积:
\[ K(\boldsymbol{x}, \boldsymbol{x}^\prime) = \phi(\boldsymbol{x})^{\top}\phi(\boldsymbol{x}^\prime). \]
举例来说,以下分别为多项式核(polynomial kernel)及高斯核函数(Gaussian kernel):
\[ K_{\text{polynomial}}(\boldsymbol{x}, \boldsymbol{x}^\prime) = (\boldsymbol{x}^{\top}\boldsymbol{x}^{\prime} + 1)^d \]
\[ K_{\text{Gaussian}}(\boldsymbol{x}, \boldsymbol{x}^{\prime}) = \exp(-\gamma\left\|\boldsymbol{x} - \boldsymbol{x}^{\prime}\right\|^2) \]
6.5.3. Random Forests
- Bagging (Bootstrap AGGregating)
- Bootstrap: 通过从样本总体中多次重复采样建立多棵决策树(Bootstrap)。
- Aggregating: 对这些树的结果进行聚合。如果树产生的结果是离散标签,则采用多数投票;如果是连续数值,则取平均。
- Random Forest: 在Bagging基础上改进,因为Bagging在每次建立决策树时考虑全部特征,而随机森林在每次建立决策树时随机选用一部分特征,这样可以进一步降低产生的每一棵决策树之间的相关性。
6.6. Clustering
6.6.1. K-means
- 随机选取k个点作为质心(centroid),每个质心代表一个聚类。
- 把每个数据点归属到离它最近的质心所代表的类别。
- 重新计算每一个聚类的质心。
- 从步骤2开始重复,直到收敛。
算法的终止条件主要有:
- 比较相邻两次迭代,如果质心没有发生变化,则算法终止。
- 比较相邻两次迭代,如果没有数据点改变其所属聚类(即被重新指派到新的质心)。
- 设置最大迭代次数。
Footnotes:
概率空间在某些特别是物理相关的著作中有时也会被叫做统计系综(statistical ensemble),这两个术语的定义可以被认为是一致的,只是由于历史原因才导致了不同的表达。统计系综是由Boltzmann于1880s提出的(若干年后亦被Gibbs采用),而概率空间是由Kolmogorov于1930s提出的。
零均值假设是因为映射后的数据方差计算 的是与均值点的相对差异,如果原始的均值点改变了,那么映射过后的数据方差 就会受影响。
\(\rho\)表示向量之间的相 关系数。
由性质\(null(\boldsymbol{X}^{\mathrm{T}}) = range(\boldsymbol{X})^{\perp}\)保证。
The goal of MLE is to find the hypothesis model that maximizes the probability of the data.
The goal of MAP is to find the hypothesis model, for which the data maximizes the probability of the model.